|
Après avoir modélisé la scène
et les objets de base il faut affiner et rendre plus réelle la qualité de l’image
d’une part en attribuant aux objets des textures ainsi que des couleurs et en
calculant d’autre part les effets d’une source de lumière dans cet environnement
de synthèse
En faite le rendu d'une image consiste à calculer
celle-ci. C'est à cette étape que l'image ou l'animation
prend toute sa dimension, les objets prennent leurs
textures et l’on calcule la luminosité.
C'est aussi à cette étape que l'on peut se rendre compte
de la qualité du travail effectué.
a)
Couleurs
Il est nécessaire pour
rendre un objet plus réaliste avant de lui appliquer une
texture de lui attribuer une couleur. Ainsi nous allons
utilisé le modèle RGB (Red Green Blue). C’est comme si
on projetait une lumière sur un objet d’un projecteur
possédant trois canaux, rouge, vert, et bleu. Ce sont
les trois couleurs de bases à partir on peut recréer
toutes les autres couleurs. Donc pour définir cette
couleur on va attribuer à chaque canal une intensité
pouvant varier de 0 à 255. Par exemple, le noir est
codé <0, 0, 0>, aucune lumière ne passant dans aucun
canal et le blanc est codé <255, 255, 255>, la lumière
blanche est composée de toutes les couleurs mais il faut
que tous les canaux aient la même intensité. Et plus ces
intensités seront forte plus le blanc sera parfait c’est
pour cela que par définition on code le blanc < 255,
255, 255 > avec des valeurs inférieures on obtient
différentes nuances de gris. Lorsque l'intensité est
maximale dans un unique canal, la couleur est dite
primaire. C'est le cas du Rouge, du Vert et du Bleu.
Quand la lumière passe par deux canaux, c'est une
couleur secondaire : le Cyan, le Magenta et le Jaune.
Les couleurs obtenues par mélange du rouge, vert, et
bleu sont rappelées par ces schémas.
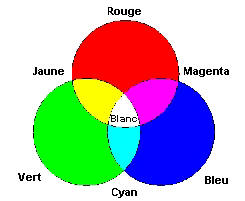
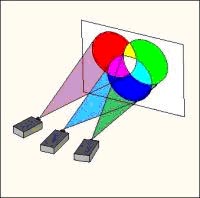
Schémas
représentant les trois canaux de couleur
Nous
avons réalisées toutes ces images :
|
Le bleu codé : rgb < 0, 0, 1 >

|
Le vert codé : rgb < 0, 1, 0 >

|
|
Le rouge codé : rgb < 1, 0, 0 >

|
Le noir codé : rgb < 0, 0, 0 >
 |
Voici
maintenant les mélange de couleur afin d’obtenir de
nouvelles couleurs :
Le blanc
codé : rgb < 1, 1, 1 >
Le jaune codé : rgb < 1, 1, 0 >


Pov-Ray le logiciel que nous avons utilisé pour réaliser
les images ci dessus comprend le RGB, mais le simplifie
: l'intervalle d'intensité n'est pas compris entre 0 et
255, mais entre 0 et 1, 1 correspondant à l'intensité la
plus élevée (c'est la notation utilisée ci-dessus). De
plus, afin d'alléger le programme, il possède une gamme
de plus de 120 couleurs "prédéfinies " dont une
vingtaine de niveaux de gris. Il suffit de donner le nom
de la couleur souhaitée et il peut l'appliquer ; cela
évite de perdre du temps pour trouver la bonne couleur
en variant l’intensité des trois canaux. On peut ainsi
définir la couleur de chaque objet ou de chaque facette
dans notre image de synthèse. On définit l’objet puis on
lui implique la couleur voulue ce qui est une étape vers
l’aspect réaliste de l’objet.
Mais pour approfondir cette intension réaliste il reste
une étape qui est très importante dans le rendu de
l’objet. Pour donner à l’objet un aspect plus
particulier, il faut lui appliquer une texture.
retour en haut
b)texture
Pour expliquer simplement, la texture que l’on applique
à un objet c’est une image (en 2D) que l’on va coller
sur chacun des polygones, afin que l’objet dans son
ensemble ait un aspect spécifique comme la pierre, le
bois…. Et c’est ici que la décomposition de l’objet en
polygone va s’avérer efficace. Car comment pourrons nous
coller cette image 2D sur une sphère parfaitement
ronde! (Heureusement il existe des formes de projection
spéciales pour traiter ces objets)
Et oui il existe plusieurs cas de projection de textures
: planaire (chaque face est un plan à part entière),
sphérique, cubique, cylindrique... Lorsque l'image est
petite, le motif est reproduit sur la face par
translation.
La couleur d'un point de la facette devient donc la
couleur du pixel de la texture. L'objet peut alors être
" recouvert " par une photo, ou avoir l'aspect du bois,
du métal, de la pierre ou même du verre.
En faite lorsque l’on applique une texture sur une
surface cela s’appelle le
Mapping :
Ainsi
Pour plaquer une texture sur un objet on utilise le
mapping (on doit indiquer à l'ordinateur comment l'on
veut que l'image s'enroule autour de notre objet. Il
existe plusieurs types de mapping dont les principaux
sont:
-Le
mapping planaire: l'image est projetée selon un plan
-Le
mapping cylindrique: l'image est enroulé autour d'un
objet cylindriquement
-Le
mapping sphérique: on applique l'image en la projetant
sphériquement

Le bump mapping, introduit par Blinn en 1978, est aussi
appelé placage de relief. Il simule des perturbations
sur une surface, créant ainsi l'illusion de creux et de
bosses sans toucher à la structure géométrique des
objets. C'est pourquoi les images utilisées pour le bump
mapping sont généralement en niveaux de gris.

Chaque niveau de gris correspond un niveau de
perturbation : les zones sombres seront en creux,
et les zones claires simuleront les bosses (par
convention). On associe généralement la texture mapping au bump
mapping pour représenter des surfaces rugueuses (roches,
murs, sols).
réflexion
et bump mapping
On pourra aussi citer l’opacity mapping, le shininess
mapping, le specular mapping, le
self-illumination mapping, le refraction et
le reflection mapping…
Le réalisme d'un objet dépend donc particulièrement de
sa texture, comme on peut le constater avec les effets
spéciaux du cinéma ou dans les jeux vidéo.
Mais Pov-Ray possède de nombreuses textures
prédéfinies toujours dans le but de rendre la
création d’une image de synthèse plus rapide ( par
exemple pour le granite, on devra juste appliquer à
l’objet « texture { granite } le logiciel Pov Ray
reconnaîtra cette texture et l’appliquera directement
à
l’objet. Il existe donc différents types de bois, de
métaux, de verres, de pierres, etc. ..., mais il est
aussi possible de les modifier en définissant par
exemple leurs indices de réfraction, de réflexion, leur
transparence, etc.…
|
Une sphère qui a l’aspect d’une
bille de métal
 |
Une sphère qui
ressemble a une boule de
granite
 |
|
une sphère de texture « mat »

|
Un cylindre et une
sphère d’aspect translucide
 |
Le
réalisme d'un objet dépend donc particulièrement de sa
texture, comme on peut le constater avec les effets
spéciaux du cinéma, ou dans les jeux vidéo.
Voici
des exemples dans le domaine des jeux vidéo :
Ainsi notre objet et l’aspect de l’image de synthèse
paraissent déjà plus réels car ils ressemblent à des
éléments et matières qui existent dans la vie réel. Mais
il manque encore quelque choser car un objet peut
toujours avoir une texture réaliste, dans un
environnement neutre il ne sera pas mis en valeur. Cela
nous amène à parler de l’éclairage que l’on peut créer
dans une image de synthèse qui va être la touche finale
du créateur.
Schéma :

retour en haut
c) éclairages
Pour modéliser l’éclairage provenant de n’importe quelle
source lumineuse dans un environnement de synthèse, on
peut utiliser différents procédés :
Modélisation
de la lumière :
Et oui sans lumière les couleurs et les textures d’un
objet ne seront pas mis en valeur ce dernier paraîtra
noir. Ainsi nous allons étudier différents moyens qui
permettent de synthétiser cette lumière dans notre
scène.
1) La
lumière ambiante
La
lumière ambiante correspond au modèle le plus simple. On
considère qu'il existe une source lumineuse présente
partout et qui éclaire de manière égale dans toutes les
directions. Chaque point de l'écran (pixel) reçoit une
quantité E de lumière égale en tous points.
Ce
modèle de lumière correspond au niveau minimum
d'éclairage qui sera appliqué sur les objets. En terme
physique cela correspond un peu au soleil réfléchi par
tout l'environnement qui donne une sorte de lumière
présente partout.
Prenons
un objet fait d'une matière unique si E reste
constant sur la totalité de l'objet. Dans ce cas,
l'objet apparaît d'une seule et même couleur. Ce modèle
d'illumination ne met pas en valeur le volume d'un objet
comme vous pouvez le voir sur la figure qui suit.

2)
La réflexion diffuse
Mais reproduire la lumière ambiante dans une scène ne
donne pas un aspect réaliste il permet juste d’éclairer
la scène car il ne prend pas en compte l’éclairement de
chaque pixel de l’image selon sa position par rapport a
la source de lumière. Une question se pose qui est de
savoir comment un ordinateur s'y prend-il pour
déterminer les points très éclairés, ceux qui le sont
moins et ceux qui ne le sont pas du tout ?
On prend comme hypothèse que la source de lumière est
ponctuelle et qu'elle émet de manière constante dans
toutes les directions de l'espace.
Dans le modèle de réflexion diffuse, l'intensité en un
point d'une surface dépend de l'angle formé entre le
rayon de lumière qui touche le point de la surface et la
normale à la surface. Plus l'angle formé entre le rayon
de lumière et la normale au plan est faible, plus
l'intensité lumineuse réfléchie visible par
l'observateur est forte.
Le
principe physique qui se cache derrière ce modèle est
simple. Notre source lumineuse émet une certaine énergie
au mètre carré. Suivant l'incidence des rayons lumineux,
cette énergie sera répartie sur une plus ou moins
importante surface de l'objet. Si les rayons et la
surface sont perpendiculaires, alors l'énergie lumineuse
sera répartie sur la plus petite surface possible et
donc l'énergie par unité de surface sera maximale (voir
figure).

La lumière émise en direction de l'observateur dépend
donc de l'intensité de la source lumineuse
E, de
l'angle
thêta
formé par le rayon de
lumière et la normale au plan et du coefficient de
réflexion
k
(facteur qui change
selon les propriétés de la texture, par exemple il va
être plus grand sur une texture de verre que sur une
texture de granite)de la lumière diffuse par la surface
et la
Couleur (x ;
y)
correspond
à l'intensité de la lumière résultant de la réflexion
sur la surface. Ainsi le programme calcule l'intensité
de la lumière pour chaque point de l'écran, en
parcourant les pixels x (abscisse) et y (ordonné), soit
l’aspect de la couleur et de la luminosité du point. On
obtient la formule :
Couleur (x ; y)
= k x E x cos
(thêta)
Schéma :
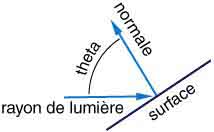
Ce schéma illustre bien
l’éclairage d’un point donné selon thêta l’angle qui est
ici l’angle i
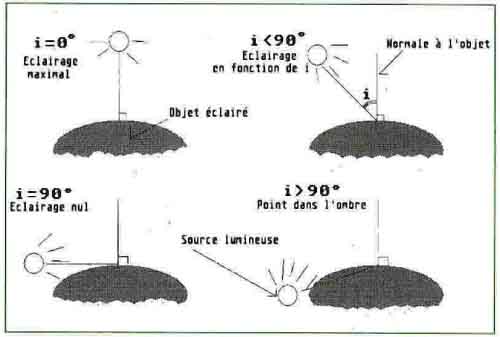
On voit de plus sur ce schéma que plus i (donc
thêta) est petit, plus il se rapproche de la normale
plus l’éclairage va être fort. Au contraire plus l’angle
se rapproche de 90 ° plus l’éclairage va être faible.
3) La
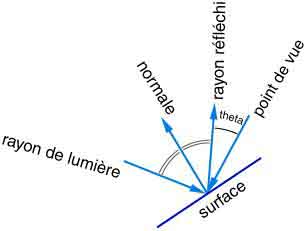
réflexion spéculaire
Le modèle de réflexion spéculaire se différencie du
modèle de diffusion en faisant intervenir le point
d'observation. Dans ce modèle les rayons de lumière sont
réfléchis par symétrie par rapport à la normale à la
surface.
Mails
la lumière diffuse ne permet pas de donner un aspect
très réel a cet éclairage, pour se rapprocher de la
réalité on peut utiliser les principes de l’éclairage
spéculaire ou la différence a la précédente loi c’est
que la position de l’observateur entre jeu dans le
calcul de la luminosité. Nous allons expliquer ce
nouveau principe:
La nouvelle formule s’écrit
Couleur (x ; y) = [k
x
>cos(i)
+w
x
n
>x
cos(theta)]
x
E
Par
rapport à la formule de Lambert, on a rajouté la mesure
de la lumière spéculaire qui dépend de l'angle thêta
(qui n’est pas le même que tout a l’heure) fait par
l'œil de l'observateur et l'objet et de deux
coefficients w, qui dépend de l'angle i,
et n, de la brillance de l'objet concerné.
La lumière réfléchie est à son maximum quand
l'angle avec la normale est égal à l'angle du rayon
d'incidence. C'est à dire lorsque thêta = i.
Plus s est grand et moins la lumière en ce point paraît
forte.
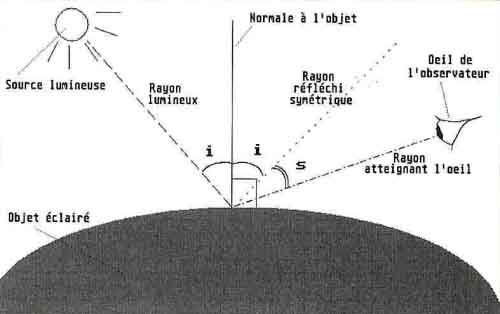
Pour
l’étude d’une image de synthèse ce schéma est plus
approprié pour comprendre ce phénomène :
4
)
Des sources multiples
|
Dans une image de synthèse on peut aussi
mettre plusieurs sources de lumière. Chaque
source doit être prise en compte dans la couleur
des pixels de l'écran. Il suffit donc
d'additionner toutes les formules issues de
chaque source de lumière plus la lumière
ambiante. Ainsi pour une scène éclairée par un
nombre l de sources, on aura la formule :

La seule différence avec la formule précédente
est l'ajout de A, la valeur de la lumière
ambiante égale en tous points. |

On remarque les deux ombres qui
prouvent la présence de deux sources de lumière. |
5
)
Les modèles d'ombrage
Maintenant nous savons calculer l’intensité lumineuse en
un point, nous allons voir les différents moyens de
calculer l’intensité de la lumière par rapport à un
polygone ce qui permet de simplifier le calcul de
l’éclairage sur un objet de synthèse, mais de le rendre
moins précis.
Il existe plusieurs façons de procéder pour approximer
la lumière en un point. On va voir les plus courantes.
L'ombrage plat
On
commence par la méthode la plus simple. On calcule la
lumière pour un seul point de la surface que l'on veut
représenter et on utilise la même intensité pour toute
la surface. Cette méthode à tendance à beaucoup faire
ressortir les polygones qui représentent un objet.
L'ombrage de Gouraud
Le
principe de l'ombrage de Gouraud est de calculer
l'intensité de la lumière pour les sommets du polygone
et d'interpoler linéairement l'intensité des sommets
pour déterminer l'intensité en un point de la face.
L'interpolation linéaire se fait sur le polygone
projeté.
Cette
technique d'ombrage ne permet pas de voir un point
lumineux qui serait au centre d'une face par exemple car
on ne calcule la lumière qu'aux sommets.
L'ombrage de Phong
Découvert en 1973 L'ombrage de Phong est assez
similaire à l'ombrage de Gouraud à la différence près
que ce n'est pas l'intensité lumineuse des sommets que
l'on interpole linéairement sur le polygone 3D mais ce
sont les normales des sommets.
Le
raytracing :
Après avoir modéliser la scène, il faut calculer l'image
ou l'animation correspondante. Pour ce faire, nous
pouvons utiliser le rendu en raytracing. Ce type de
rendu existe depuis de nombreuses années. C'est une
méthode permettant d'obtenir des résultats très
réalistes à condition de bien avoir paramétré sa scène.
Connu en français sous le nom de "lancer de rayons",
"tracé de rayons" ou encore "suivi de rayons", la
raytracing est une technique de rendu d'images photo
réalistes, dont les effets utilisent -autant que
possible- les propriétés optiques des lumières, objets
et matériaux.
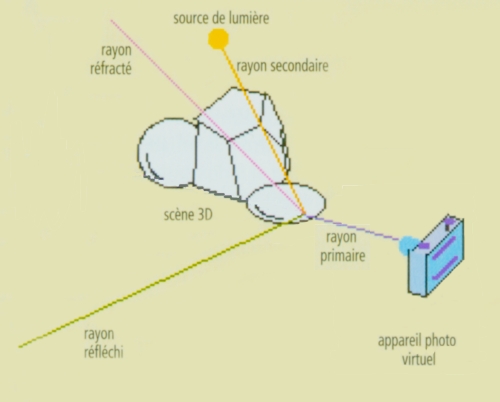 .
.
On projette un rayon lumineux, appelé rayon primaire,
partant de l'œil de l'observateur (ou caméra, appareil
photo virtuels) et passant par chaque pixel de l'écran
de manière à déterminer si ce rayon intercepte un objet
de la scène. Deux cas sont alors possibles :
- Aucun objet n'intercepte le rayon, la couleur est
celle du fond.
- Des objets interceptent le rayon, seul l'objet le plus
proche de l'observateur est pris en compte, la teinte du
pixel est calculée en fonction des caractéristiques de
la texture (valeur diffuse, réfléchie et réfractée).
Voyons maintenant quels sont les principes utilisés pour
calculer les équations des droites permettant d'évaluer
l'intensité lumineuse d'un point.
La
diffusion
:
Pour calculer l’intensité de la lumière pour chaque
pixel on utilise les principes de la diffusion de la
lumière, on va lancer des rayons, appelés rayons
primaires, à partir de l'œil et qui passe par un
pixel de l'écran
|
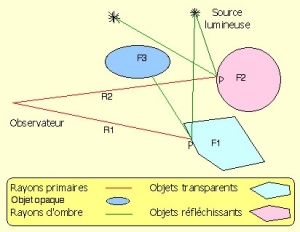
Pour chaque rayon R (ici rayon rouge) lancé
de l'œil, on calcule le premier objet F qu'il
intercepte. Une fois ce premier objet trouvé, il
faut déterminé la couleur du pixel à afficher.
Celle-ci dépend du matériau de la face, sa
texture, et bien sûr de l'éclairage. Donc il
faut déterminer quelles sont les sources
lumineuses qui éclairent le point P de l'objet
rencontré par le rayon primaire. Mais pour
savoir si ce point est éclairé, on trace un
rayon provenant du point jusqu'à la source
lumineuse et si ce rayon est intercepté par un
objet (ici F3) alors il s’agira d’une zone
d’ombre. Et le point P sera à l’ombre. |
 |
Donc si ce rayon parvient à la source sans intercepter
d'autre objet, alors la source contribue à l'éclairage
du point P. Dans le cas contraire, un objet masque la
source et engendre naturellement un effet d'ombre.
La
réflexion
:
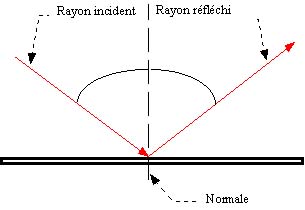
Quand un rayon lumineux rencontre une surface, celui-ci rebondit
dessus. Une partie de la lumière est directement
réfléchie par l'objet selon une trajectoire bien
spécifique.
En effet, si nous considérons la normale au point
d'impact, l'angle que fait le rayon incident (celui qui
arrive) avec cette normale est égal à l'angle entre le
rayon réfléchi et la normale.
Il est donc très facile de calculer les coordonnées de
la droite représentant le rayon réfléchi.
Néanmoins, ceci n'est plus vrai si l'objet n'est pas
lisse. Dans ce cas, il faut tenir compte des aspérités
de l'objet pour calculer la normale à celui-ci.
De même, si l'on arrive sur un angle, le calcul de la
normale est différent. On peut néanmoins faire une
approximation car atteindre précisément un angle est
assez rare.
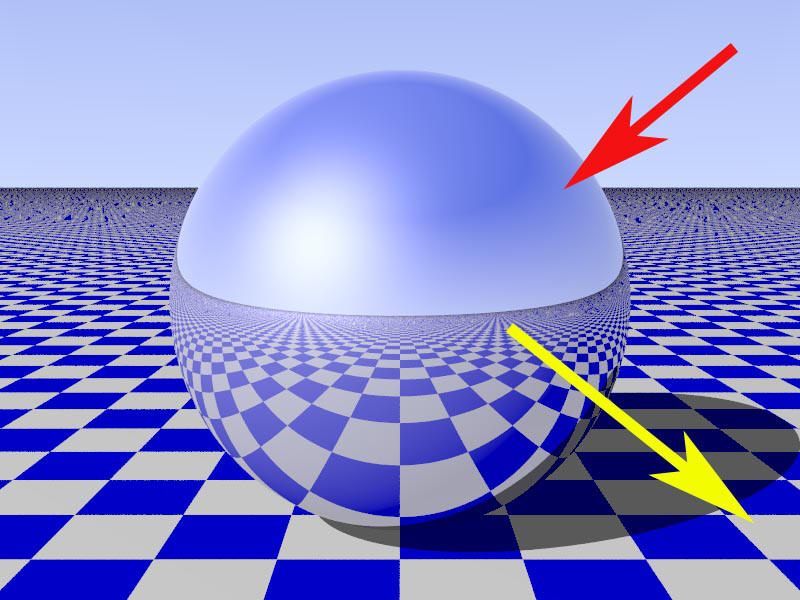
Application :
Pour
résumer le rayon primaire est réfléchi en rayon
secondaire et c’est l’objet qui réfléchi le rayon
primaire qui va refléter l’objet que le rayon secondaire
rencontre. Reprenons l’image de cette bille on
s’aperçoit que l’objet (ici le sol) que le rayon
secondaire (jaune) intercepte et refléter par la bille
en métal.
La
réfraction :
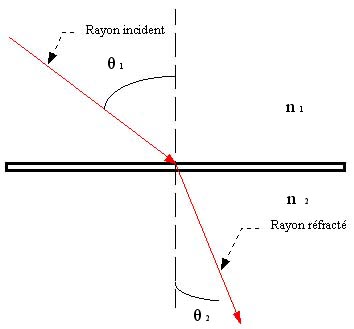
Lorsqu'un objet est transparent par exemple, il y a de
la lumière qui peut passer à travers. Donc la lumière
qui vas arriver sur cet objet (rayon incident) va être
réfractée (rayon réfracté) On applique a ce moment la
les propriétés de diffraction de la lumière. Pour
calculer cette réfraction on utilise le principe de la
loi de Descartes :

 étant
l'angle d'incidence du rayon, l'angle
de réfraction et n l’indice de réfraction des
milieux traversés.
étant
l'angle d'incidence du rayon, l'angle
de réfraction et n l’indice de réfraction des
milieux traversés.
En faite, la quantité de lumière pouvant arriver au
point d'impact dépend de l'indice de transparence de
l'objet. De plus, certains objets on des propriétés de
diffraction de la lumière. Cela signifie, que la lumière
ne passe pas en ligne droite à travers l'objet. Elle
peut être légèrement déviée par celui-ci. Cela s'observe
facilement avec l'eau : lorsqu'un objet est plongé dans
l'eau, la position à laquelle on peut le voir n'est pas
la position à laquelle il est.
Comme on peut le voir sur cette image de synthèse la
lumière qui entre dans ces objets est réfracté et donc
l’image du sol et dévié par rapport a la normal par le
rayon réfracté qui pénètre dans l’objet :

Photo-Bilan, exemple de rendu avec l’application du
raytracing:

Mais le raytracing fait partie d’un des nombreux
procédés utilisés pour synthétiser la lumière, il en
existe de nombreux autres cependant c’est celui qui
parait le plus efficace et qui comporte le moins de
désavantage…
Conclusion :
Ainsi nous avons expliquer toutes les étapes qui nous
permettent de créer une image de synthèse, et nous a
donc permis de réaliser cette image qui nous a demander
plus d’expérience que les précédentes afin d’illustrer
notre TPE :

Après toutes ces étapes nous avons réussi à créer une
image de synthèse ce qui nous permet de comprendre le
terme majeur de notre problématique, il reste maintenant
à savoir dans quels domaines on utilise et on profite des
avantages de cette technologique…
retour en haut |






























